matrix

矩阵分析与应用
课程大纲

线性方程组
高斯消元法
- 三种线性变换
- 交换两行
- 对某一行乘上一个非零系数
- 对某一行加上另一行乘以一个非零系数
- 对于一个nxn的矩阵进行高斯消元法(反向替换)需要的操作数
$\frac{n^3}{3}个乘法操作和\frac{n^3}{3}个加法操作$
- Gauss-Jordan方法
与标准的Gaussian消元法的区别:
- 所有的主元都为1
- 除了主元其他元素都为0
复杂度和标准Gaussian消元法相同
部分主元法和完全主元法
- 部分主元法:
- 主元位置的元素为主元所在列的最大的一个值
- 完全主元法:
- 主元位置的元素为主元所在列和行所包围的下半部分的最大的一个值
病态系统
一点扰动对整个系统的解会造成很大的影响,可视化的结果就是两条线几乎平行
- modified gaussian elimination
主元位置不再是对角线上的位置,而是从左到右第一个不为0的元素,必要情况下可以进行行交换,最终形态是某一行以及下面的所有行都为0
- 矩阵的秩的定义
- 主元的个数
- 消元后的非零行的个数
- Basic columns的个数(Basic columns指的是包含主元的列,注意的是Basic columns是原始矩阵中的列,不是消元后的列)
- reduced row echelon form
- 首先是row echelon form
- 每一行第一个非零元素是1
- 主元所在列除了主元其他都是0
- basic columns可以用来表示nonbasic columns
- 线性系统的一致性
只要有一个解,则称这个线性系统是consistent,否则是inconsistent

- Homogeneous Systems(齐次系统)
齐次系统和非齐次系统的解的情况:

矩阵代数
矩阵加法和转置













向量空间


















- rank(A) = the size of the largest nonzero minor of A
线性变换







模和内积
- Induced matrix norms

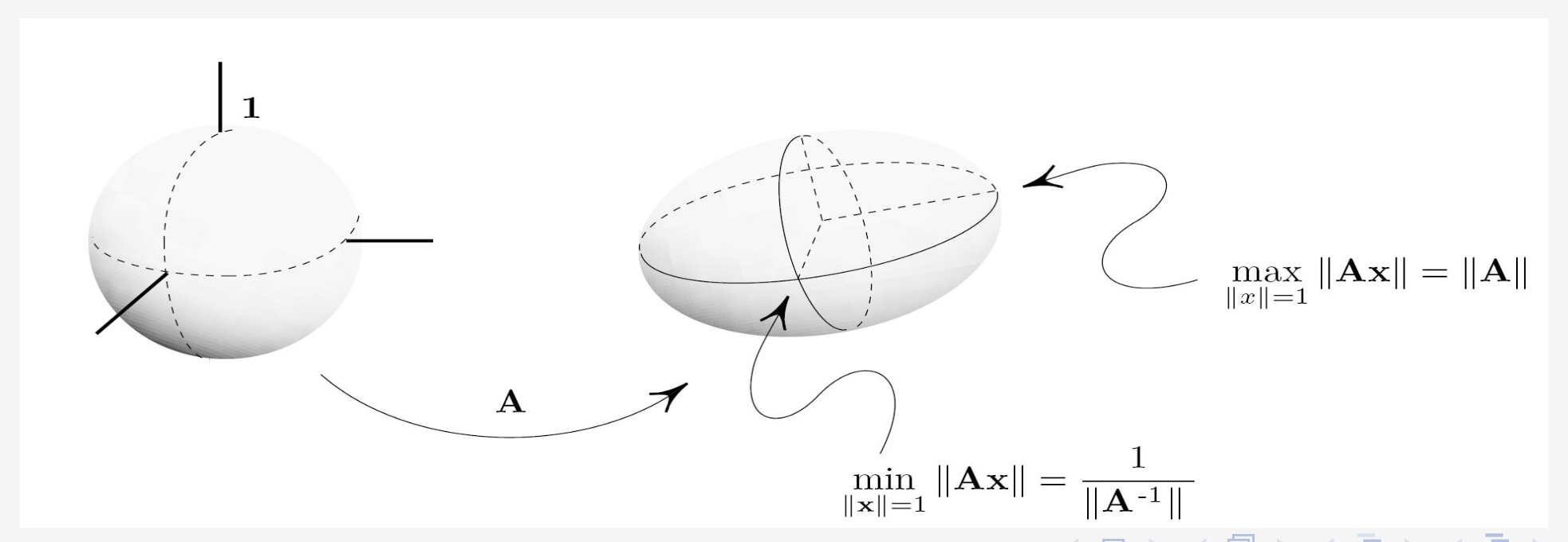
- 2-Norm


- 1-norm
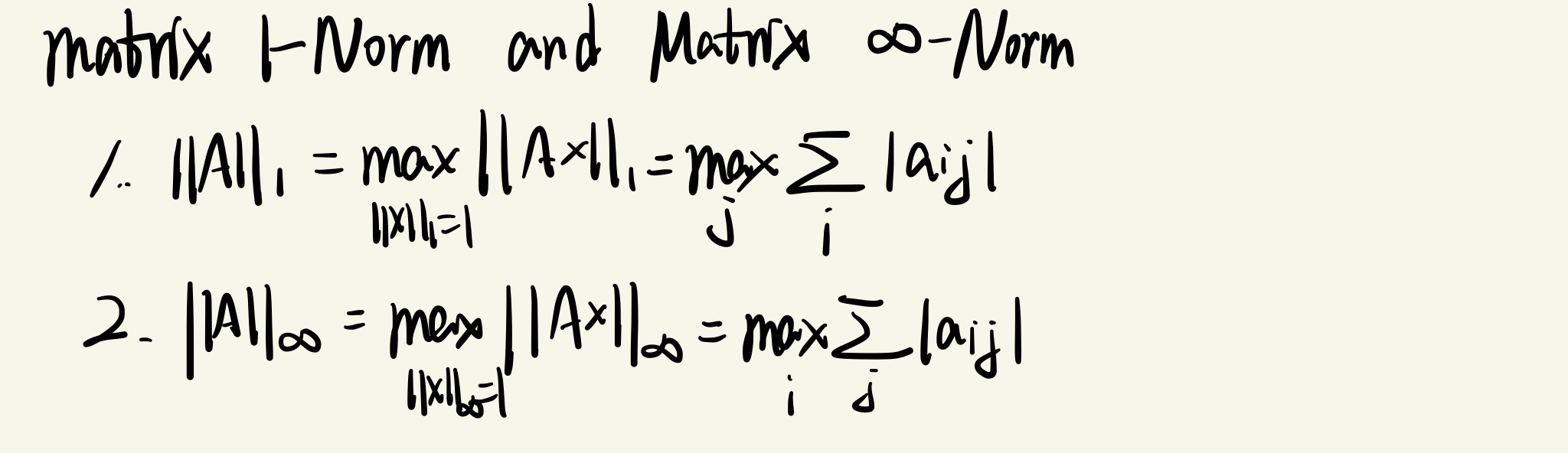
- 内积空间

- general inner product
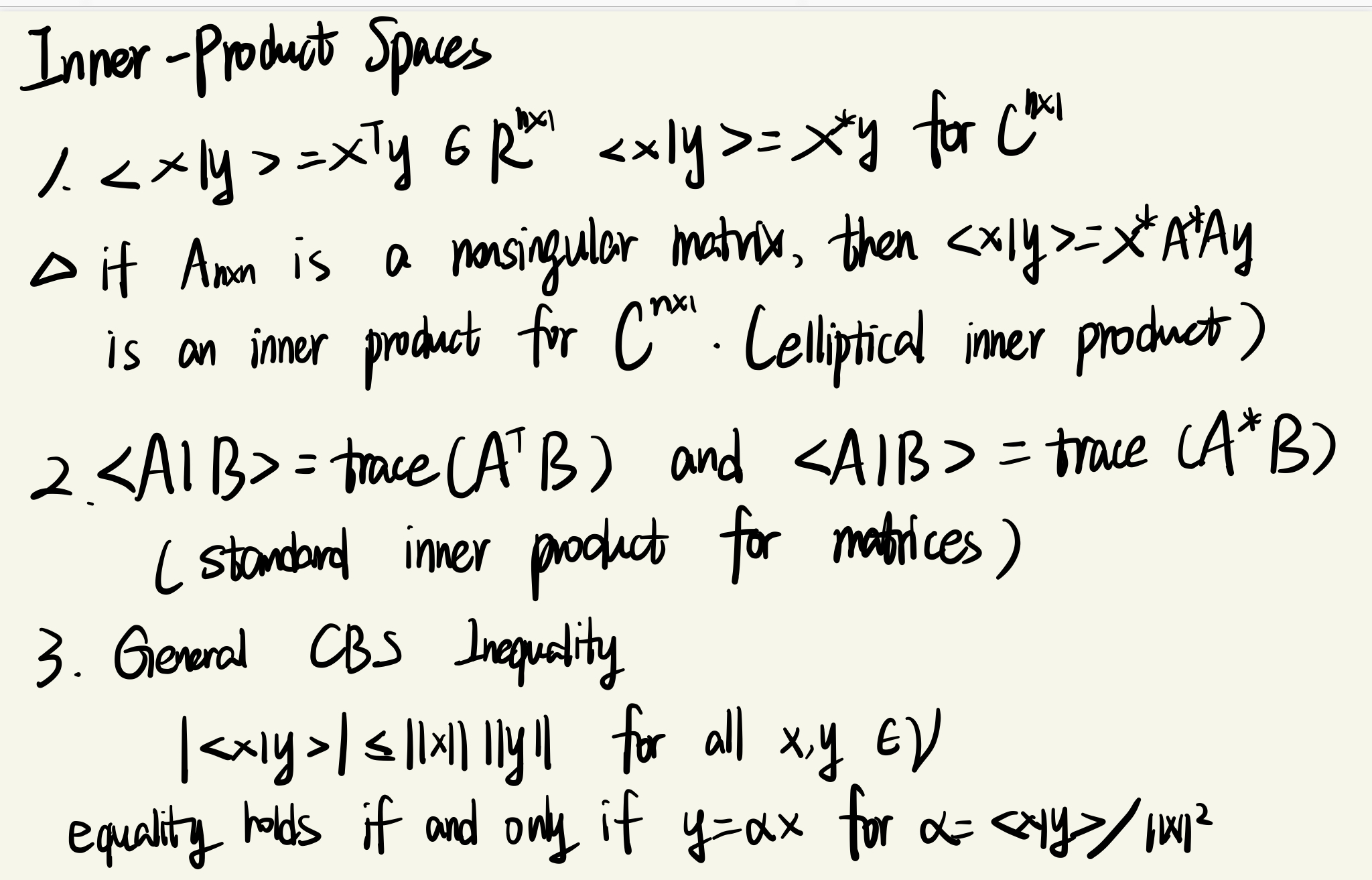

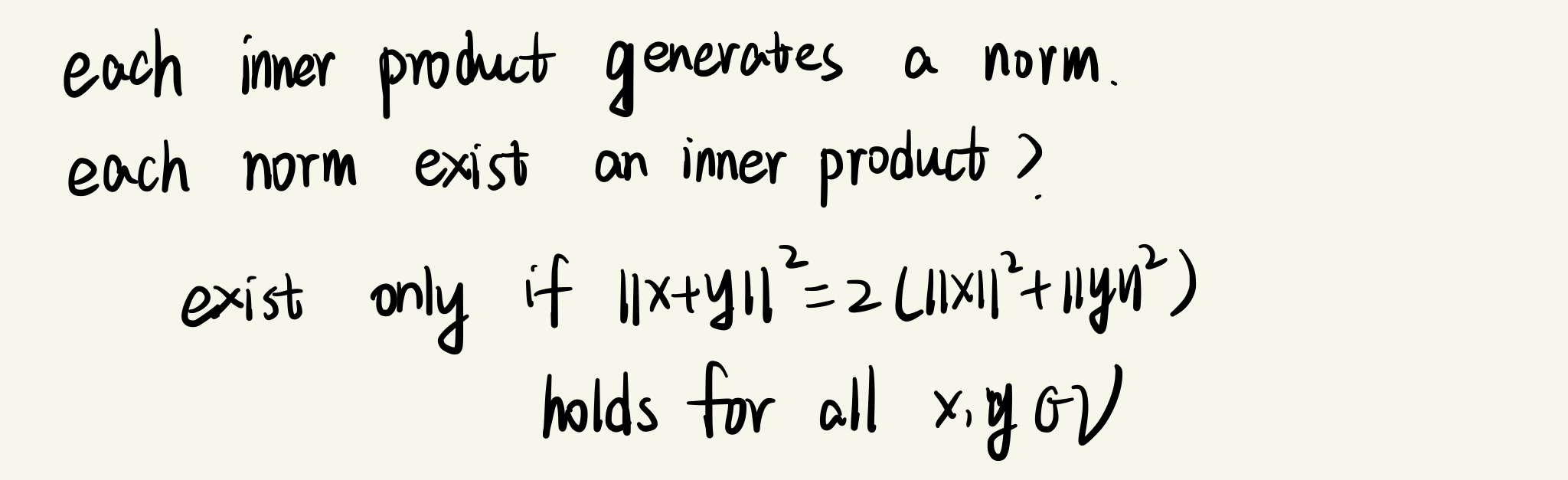
- 正交向量
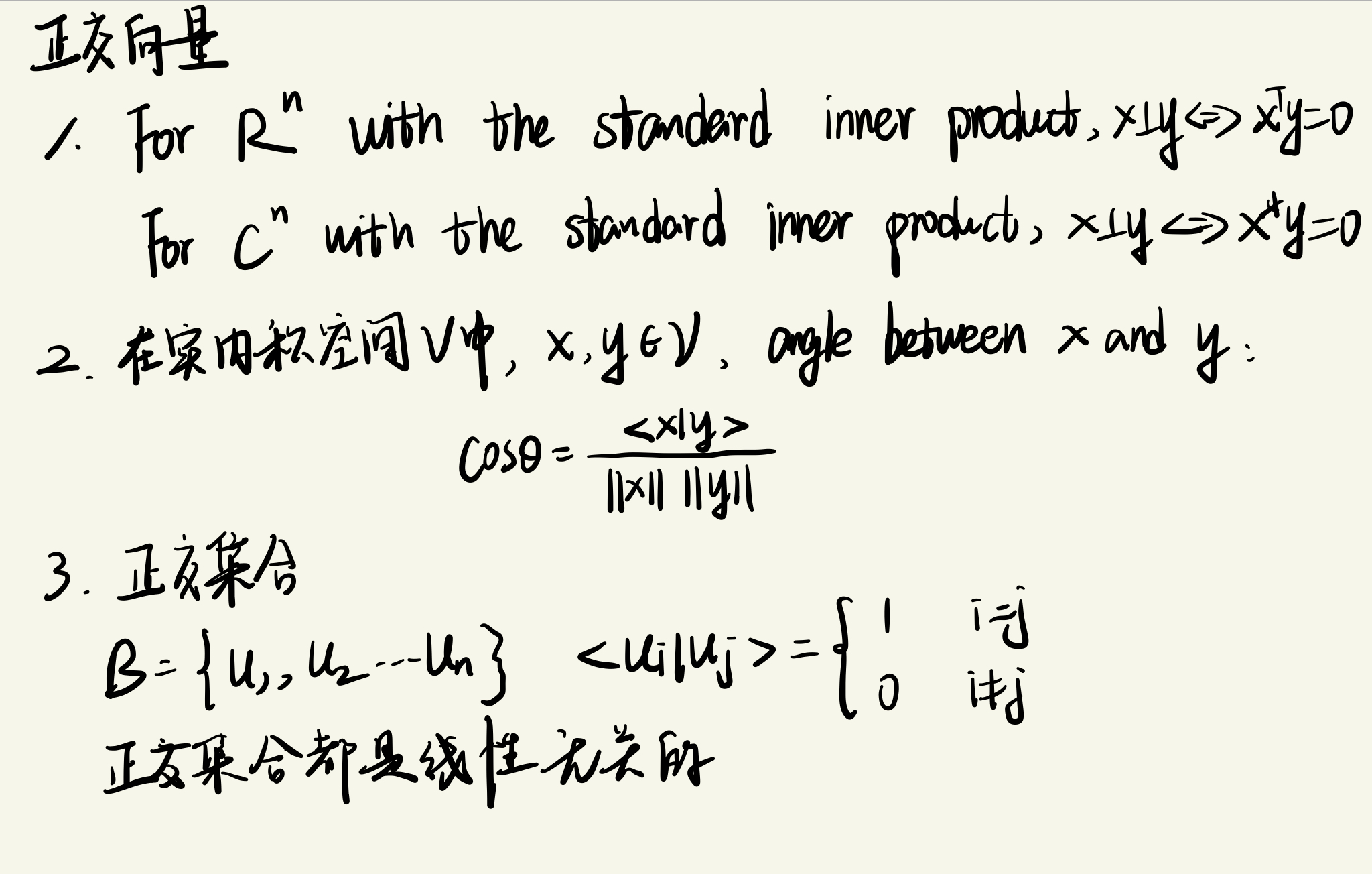

- Gram-Schmidt Procedure




- Unitary and Orthogonal Matrices(酉矩阵)





- Orthogonal Reduction


DFT
余子空间


- RN分解




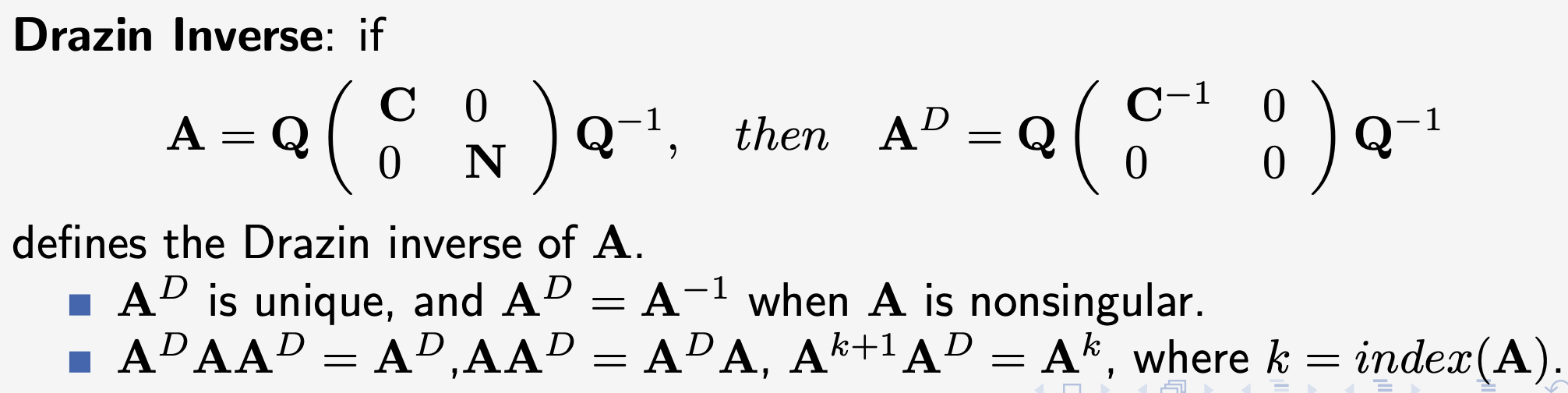
- 正交分解




- 奇异值分解

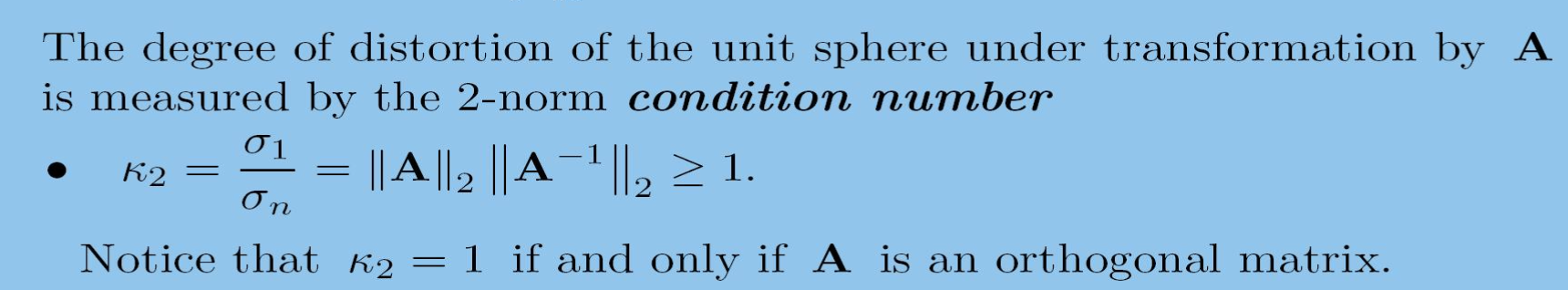


- 正交投影


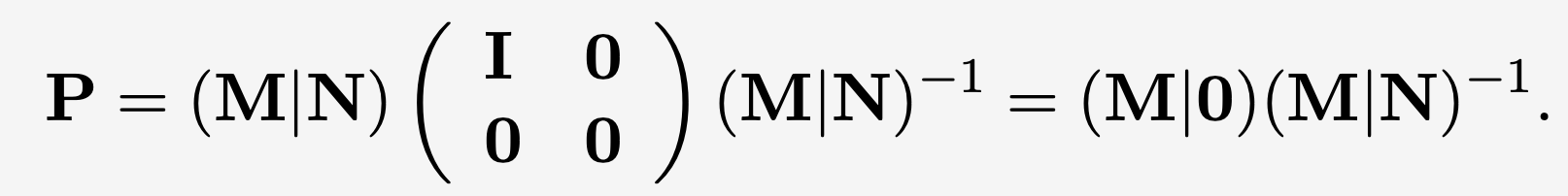
行列式
- 只有方阵才有行列式
- 转置不影响行列式的结果

$$
det(PA) = det(P)det(A),无论P是哪个元素变换
$$
- 矩阵内积的行列式(方阵)
$$
det(AB) = det(A) det(B)\
det\left(
\begin{array}{cc}
A &B\
0 &D
\end{array}
\right) = det(A)det(D)
$$


行列式的求导

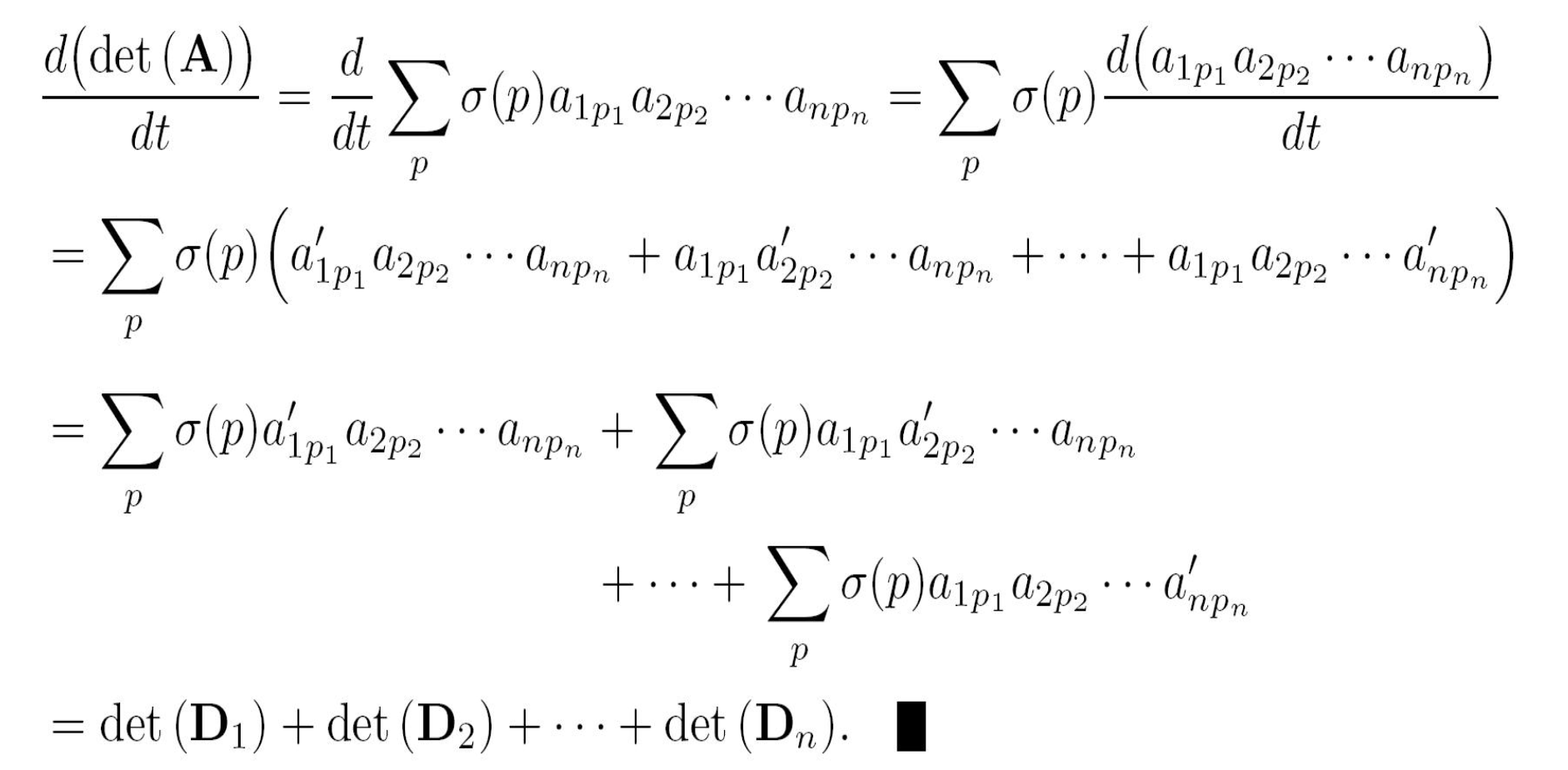
- 分块行列式

- Rank-1行列式

- 利用cofactor计算行列式和逆
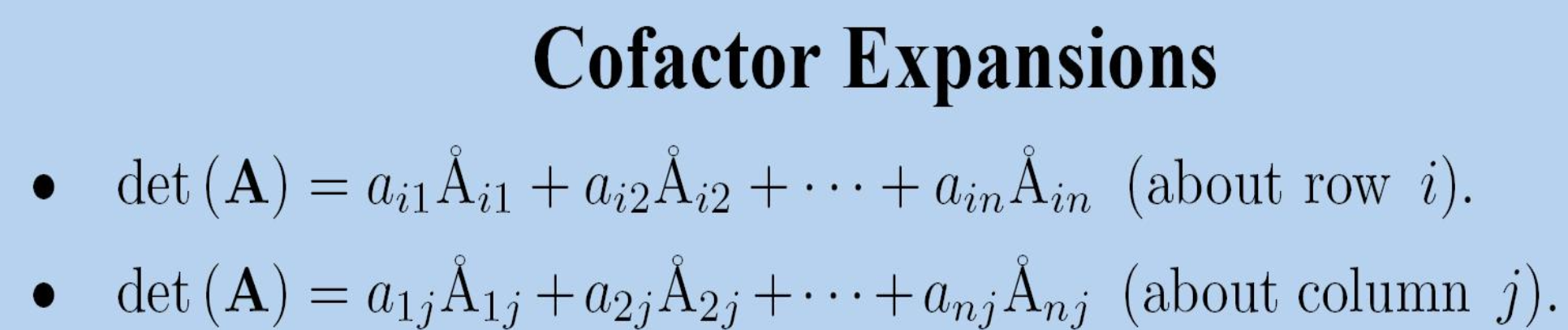

特征值和特征向量
- 关于特征值和特征向量

- 特征式的系数

- 对角化

- Multiplicty

- diagonalizability

- 对角化的必要条件及谱分解



- normal matrix



- positive definite matrices

正定矩阵的定义:

半正定:

二次型:

合同变换

一些注意点
- 完备空间的证明除了互补之外还要证明唯一性

- Post title:matrix
- Post author:calcium_oxide
- Create time:2022-11-05 13:53:43
- Post link:https://yhg1010.github.io/2022/11/05/matrix/
- Copyright Notice:All articles in this blog are licensed under BY-NC-SA unless stating additionally.