multi-ml

百面机器学习

特征工程

1. 训练数据不足时带来的问题以及如何缓解？

一个模型能够提供的信息一般来源于两个方面：

• 训练数据中蕴含的信息
• 在模型的形成过程中人提供的先验信息

当训练数据不足时，模型从原始数据中获得的信息比较少，模型容易过拟合，在这种情况下就需要更多的先验信息。先验信息可以作用于模型，对模型进行简化、添加正则项、dropout等进行约束，也可以作用于数据，在保持特定信息的前提下，对原始数据进行适当变换以扩充数据集，在图像任务中有以下一些操作：

• 一定程度内的随机旋转、平移、缩放、裁剪、填充、左右翻转等

• 对图像中的像素添加噪声扰动（高斯、椒盐噪声）

• 颜色变换（在图像的RGB颜色空间上进行主成分分析，得到3个

  主成分的特征向量p1、p2、p3 及其对应的特征值 λ1,λ2,λ3，然后在每个像素的RGB值上 添加增量[p1 ,p2 ,p3 ]•[α1 λ1 ,α2 λ2 ,α3 λ3 ]T，其中 α1 ,α2 ,α3 是均值为0、方差较小的高斯分布随机数）

• 改变图像的亮度、清晰度、对比度、锐度等

除了直接在图像空间上进行变换，还可以先对图像进行特征提取，然后在图像的特征空间内进行变换，利用一些通用的数据扩充或上采样技术，例如 SMOTE(Synthetic Minority Over-sampling Technique)算法。还可以使用生成模型合成一些新样本。

迁移学习也是一种常用的策略（微调）。

---

模型评估

1. 一些常用的指标：

• 准确率

$$
Accuracy = \frac{n_{correct}}{n_{total}}
$$

其中ncorrect为被正确分类的样本个数，ntotal为总样本的个数。

准确率往往会收到不同类别样本不均衡带来的问题，占比大的类别往往成为影响准确率的主要因素。

• 精确率

$$
precision = \frac{n_{分类正确的正样本}}{n_{分类器判定为正样本}}
$$

• 召回率

$$
recall = \frac{n_{分类正确的正样本}}{n_{真正的正样本}}
$$

• P-R曲线（横轴是召回率，纵轴是精确率）
• F1 score

$$
F1 = \frac{2precisionrecall}{precision+recall}
$$

• MAPE（平均绝对百分比误差）

$$
MAPE = \sum_{i=1}^{n}|\frac{y_i-\hat{y_i}}{y_i}|*\frac{100}{n}
$$

比RMSE鲁棒性更好。

• ROC曲线（横坐标为假阳性率，纵坐标为真阳性率）

$$
FPR = \frac{FP}{N}\
TPR = \frac{TP}{P}
$$

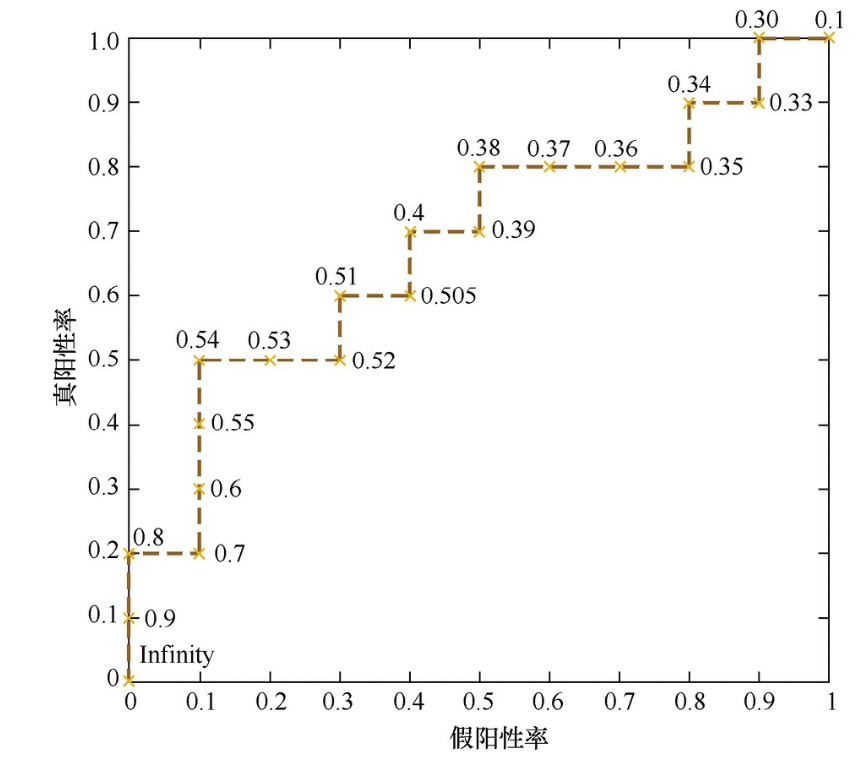
• AUC（ROC曲线下的面积，可以量化地反应基于ROC曲线衡量的模型性能），AUC越大，说明分类器越可能把真正的正样本排在前面，分类性能越好。
• 当正负样本的分布发生巨大变化时，ROC曲线的形状能够基本保持不变，而PR曲线的形状一般会发生较剧烈的变化。ROC曲线能够避免测试集带来的影响而专注于模型本身的性能，而PR曲线则可以看到在特定数据集上的表现。
• 除了对模型的评估外，也需要评估样本间的距离，在机器学习问题中，通常将特征表示为向量的形式，所以在分析两个特征向量之间的相似性时，常使用余弦相似度来表示。余弦距离则是用1减去余弦相似度来表示。因为余弦相似度在高维情况下仍然可以保持相同为1，正交为0，相反为-1的性质，而欧式距离的数值则会受到维度的影响，范围不固定并且含义也比较模糊。
• 关于距离的定义：正定性、对称性、三角不等式，余弦距离不满足距离的定义，另外KL距离也不满足对称性和三角不等式

2. 模型评估的方法

• holdout检验（训练测试七三开）
• 交叉检验
• 自助法（对于总数为n的样本集合进行n次有放回的随机抽样，得到大小为n的训练集，n次采样过程中没有被抽出过的样本作为验证集）（在n趋于无穷大时，大约有36.8%的样本从未被选择过）

3. 超参数调优

• 网格搜索
• 随机搜索
• 贝叶斯优化算法

贝叶斯优化算法首先根据先验分布假设一个搜集函数，每一次使用新的采样点来测试目标函数时，利用这个信息来更新目标函数的先验分布，最后算法测试由后验分布给出的全局最值最可能出现的位置的点。主要就是引入了先验分布，通过不断采集数据得到后验来预测最值。

4. 过拟合与欠拟合

• 过拟合

  • 通过数据增强获得更多数据
  • 降低模型复杂度，减少网络层数、神经元个数等
  • 正则化方法，将权重加入到损失函数中
  • 集成学习方法，将多个模型集成到一起

• 欠拟合

  • 添加新特征，通过特征组合、挖掘上下文特征
  • 增加模型复杂度，在神经网络模型中增加网络层数或神经元个数等
  • 减小正则化系数

---

经典算法

1. 支持向量机

问题1： 在空间上线性可分的两类点，分别向SVM分类的超平面上做投影，这些点在超平面上的投影仍然是线性可分的吗？

==优化问题：==

• 无约束条件
  • 函数对变量进行求导求极值点
• 等式约束条件
  • 拉格朗日乘子法，在目标函数中加入等式约束
  • 对拉格朗日法的理解：等式约束可以看做是曲面上的一条等高线，而目标函数则是随机一条约束，在等式约束下的目标函数的极值就是等高线和约束的相切点，两者的梯度在一条直线上
• 不等式约束条件
  • 对于一般问题，KKT条件是使一组解成为最优解的必要条件，当原问题是凸问题时，也是充分条件

==超平面分离定理==：

对于不相交的两个凸集，存在一个超平面，将两个凸集分离

根据超平面分离定理，可以求两个凸集的凸包，SVM求得的超平面就是两个凸包上距离最短的两点连线的中垂线

问题2：是否存在一组参数使SVM训练误差为0？

存在，可以通过构造一个高斯核函数以及相应的参数控制预测值和真实值的误差在0-1之间，因为gt只有1和-1，则无论何种情况都可以全部正确分类（高斯核占主导）

问题3：训练误差为0的SVM分类器一定存在吗？

可以找到一组参数满足训练误差为0，且是SVM模型的一个解（超参数占主导）

问题4：加入松弛变量的SVM的训练误差可以为0吗？

因为优化的目标改变了，优化的目标函数里面包含松弛变量的正则项和间隔，所以训练误差不一定能达到0

2. 逻辑回归

问题1：逻辑回归相比于线性回归，有何异同？

• 逻辑回归处理的是分类问题，线性回归处理的是回归问题
• 逻辑回归中的『回归』来源：在逻辑回归的推导过程中存在以下形式：$log\frac{p}{1-p}=\theta^Tx$，其中$p$是『$y=1|x$』这一事件的对数几率的线性回归
• 在线性回归中因变量$y$是连续的，而在逻辑回归中因变量$y$的离散的，逻辑回归中的$y$服从二元分布，而线性回归中的$y$服从正态分布

3. 决策树

---

降维

---

非监督学习

---

概率图模型

---

优化算法

---

采样

---

前向神经网络

---

循环神经网络

---

强化学习

---

集成学习

---

生成式对抗

---

人工智能