algorithm_bu

卜东波——计算机算法设计与分析

课程大纲

第一章 建模、算法设计、分析完整流程 10学时 卜东波
第1节 掌握从问题出发的算法建模方法
第2节 掌握算法设计的基本思路和流程图
第3节 掌握算法的时间复杂度和空间复杂度分析的方法
第4节 理解GCD问题和TSP问题中不同算法的应用
第二章 分而治之 10学时 卜东波
第1节 掌握分而治之算法的基本思路
第2节 掌握分而治之算法的正确证明
第3节 掌握递归算法的时间复杂度分析
第4节 掌握MergerSort、CountingInversion、ClosetPair、Multipliacation、FFT等使用分而治之思路算法
第5节 掌握分而治之算法和随机化的结合，例如QuickSort、QuickSelect等
第三章 动态规划部分 10学时 卜东波
第1节 掌握动态规划算法的基本思路
第2节 掌握如何定义子问题，如何发现最优子结构的性质
第3节 掌握动态规划算法的应用实例，包括矩阵链式乘法、字符串匹配、最短路径、IntervalScheduling
第4节 理解高级动态规划的优化方法和思路
第四章 贪心算法 10学时 卜东波
第1节 掌握贪心算法的思路
第2节 掌握贪心算法中贪心规则的设计原则和方法等
第3节 掌握动态规划和贪心算法的关系
第4节 掌握BELLMAN_FORD算法和DIJKSTRA算法解决Single Source Shortest Paths问题
第5节 掌握BinomialHeap、FibinacciHeap等数据结构
第五章 线性规划及其对偶 10学时 卜东波
第1节 掌握线性规划的不同形式
第2节 掌握线性规划的建模思路和方法
第3节 掌握线性规划的单纯形法、Interior Point算法等
第4节 线性规划的Lagrangian对偶
第六章 网络流及其应用 10学时 卜东波
第1节 掌握最大流问题的Ford-Fulkerson算法和最大流最小割定理
第2节 掌握Ford-Fulkerson算法和最大流最小割定理的对偶问题角度理解
第3节 掌握最大流问题的有效算法
第4节 掌握最大流问题的扩展

lecture1

一些推荐的书

• 《怎样思维》
• 《程序设计的艺术》

所有的算法可以归纳为三种

• 分而治之 | 一个大问题可以分成更小的子问题
• 改进 | 一个原始的完整解，不断地逐步改进
• 聪明地枚举 | 通过构建一个局部解的树来枚举所有可能的完全解

计算思维

从最简单的情形做起，要分支、要归纳、要聪明地枚举、搜索要剪概率有力量

方法论

---

分而治之：

• 最简单的case
• 复杂一点的case是否可以分解成小问题
  • 是否能分解成子问题：
    • INPUT DS
    • OUTPUT DS

改进：

• 完整解通过一些扰动成为另一个解

聪明地枚举

• 剪枝

TAKE-HOME MSG

• 手足无措时从最简单的case做起
• 理性地探索
• 精确值难求的时候，估计之
• 找准难点，变形做相关问题

lecture5

分治和复杂度分析

---

递归问题的复杂度分析

for example:

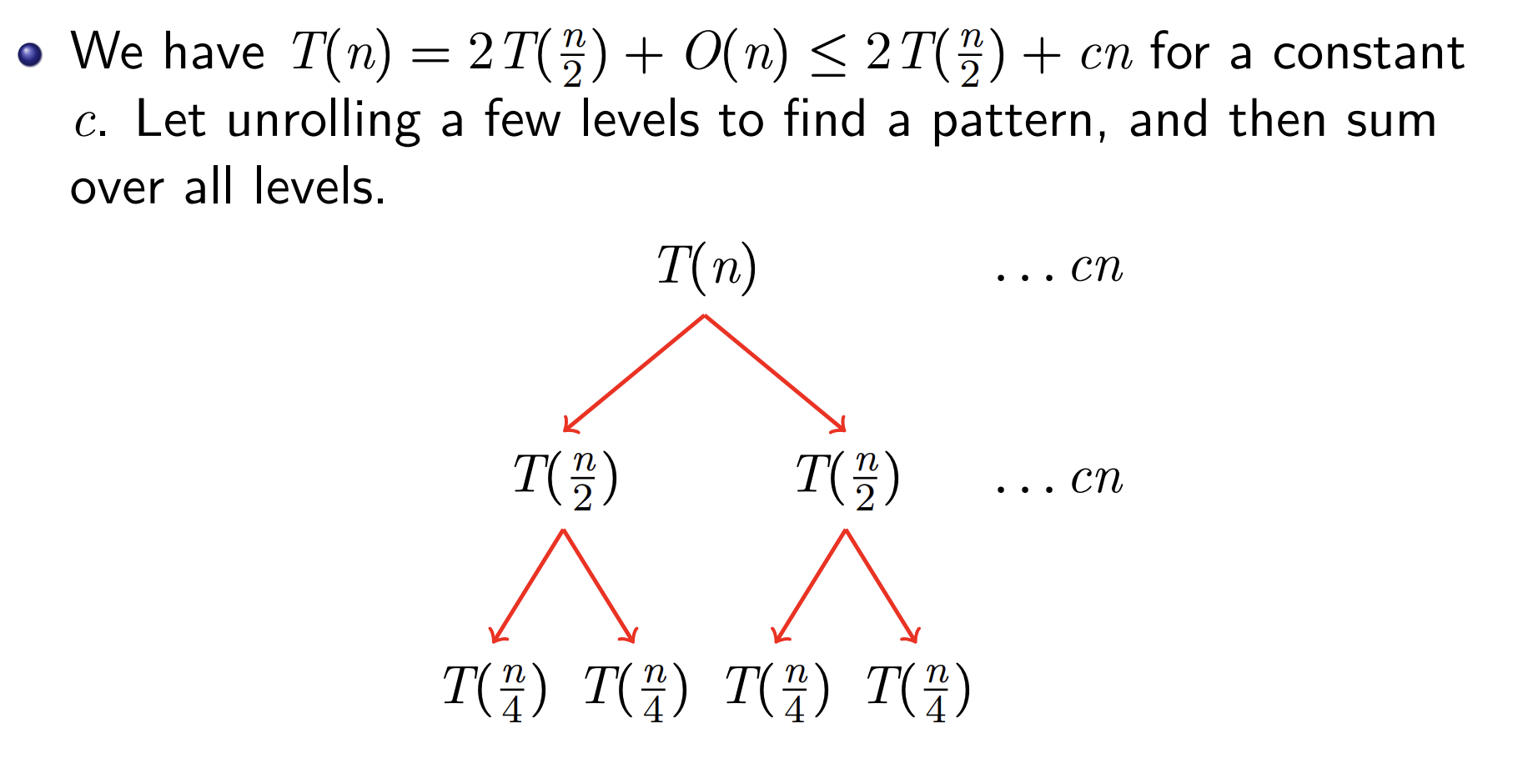
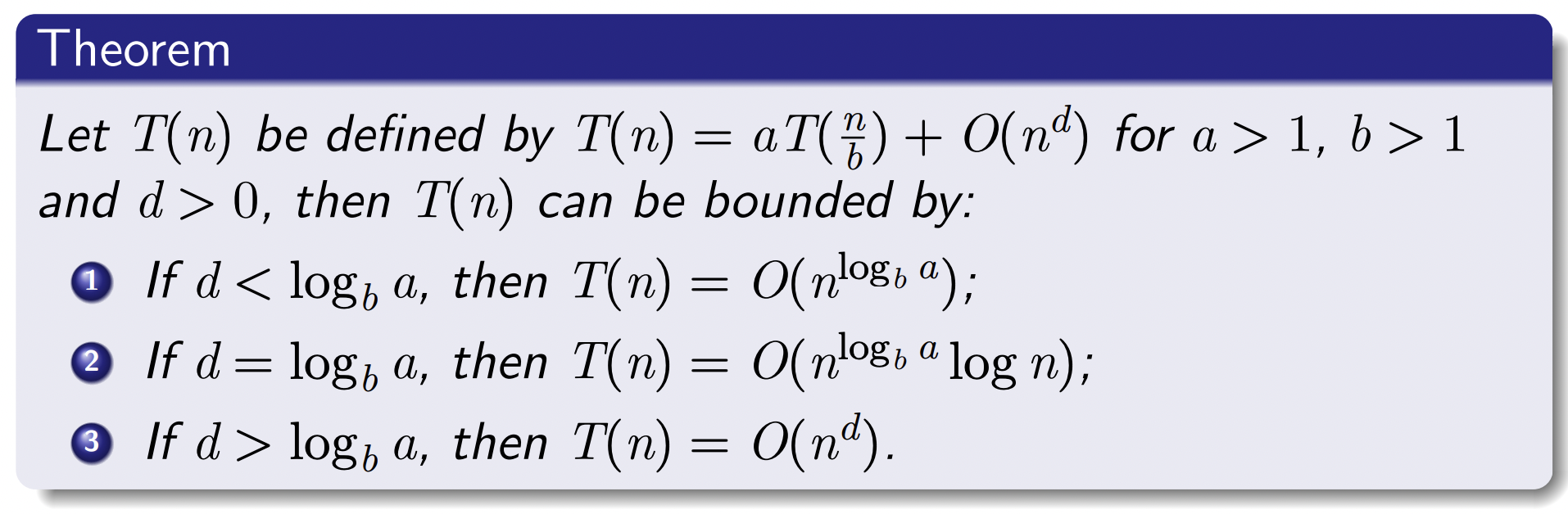
O(n)

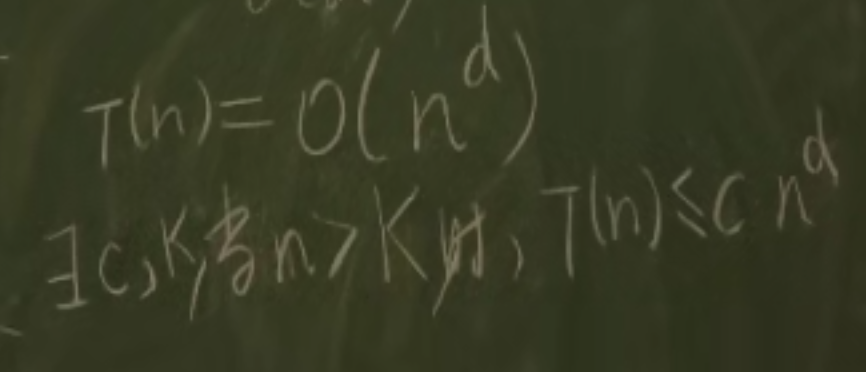
TAKE-HOME MSG

• 把大问题分解成小问题时，分得越匀越好（指数下降）
• 如果子问题解无结构，可能会导致问题，千方百计引入结构
• 先尝试baseline方法，看问题所在（逆序数个数中分治的齐缝元素比较）

quicksort

$$
\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}=logn
$$

找出第k大的元素：

使用分治来解决，时间复杂度可以达到O（N）。
在快排的基础上还是分成两个集合，只不过区别在于快排是两个集合都要递归，分治只要递归其中一个集合。

Google对页面排序：

重要的页面：常常被重要的页面引用的页面很重要（鸡生蛋，蛋生鸡问题）

解决循环：

• 跟着循环走，观察规律
• 打破循环

在子集中寻找第K大个元素（通过打破循环来找到pilot元素，从而在O（N）复杂度内实现）

关键：-》找到A中第n/4，n/4+1，3n/4个大的-》找A的采样中的第r/4，3r/4个

TAKE-HOME MSG

• 解决循环问题的两个办法
• 快排的分析

lecture5

FFT：已知多项式的系数、求多项式的值

特定的n个点：
$$
\omega^1, \omega^2…\omega^{n-1}
$$
去掉冗余，O(n^2)->O(nlogn)

IFFT

实际应用：计算两个多项式的乘积

先用FFT计算几个点的值，然后再计算这些点的乘积，再用IFFT计算对应的多项式的系数

lecture6

DP的求解过程：多步决策过程（优化问题）

TAKE-HOME MSG

• 何时用动态规划，一定是个最优化问题
• 解是啥？解能否用多步决策过程一步一步构造出来

lecture1011

• 矩阵相乘的最少计算数
• 背包问题
• 编辑距离

TAKE-HOME MSG

• 每一个多决策问题都可以表示为一个DP
• 多选一型vs二选一型决策
• 决策顺序怎么定

lecture1025

TAKE-HOME MSG

• 多步决策，第一步决策，从中间开始省内存，省时间
• 如何计算第一步决策，最优决策项？最优决策项有递归关系
• DP也可以用NN近似，不精确不要紧
• label不好算？让NN满足Bellman方程

lecture1101

TAKE-HOME MSG

• 直接根据子问题的解设计子问题的一般形式
• 有时候失败：1.循环依赖（加变量分解成更细的子问题） 2.子问题之间根本没有递归关系

作业复习

分治

• 两个集合的中位数
• 左右孩子翻转
• 越狱情况数
• 二叉树任意两个结点的最大距离
• 三路快排
• 切绳子

dp

• 抢劫金额最大
• 丑数
• 二叉搜索树的数目
• 最大整除子集长度
• 非负数组符号和为目标数的方法数（0-1背包）
• 股票买卖
• 回文子串的个数
• 单词转换所需要的最少操作数

贪心

• 填充道路
• 数组中的数字构成最小整数
• 会议室安排
• 删除k个数字得到的数最大
• 是否可以到达最终的位置
• 交换数字索引得到最大值
• 最大极差和

线性规划

整数规划